This is the second in a series of blogs following Kay Lack’s ODE5 (pronounced odez)

ODE5 is a project to rekindle the excitement everyone first experienced about computer science and problem solving, but most of us have not had the chance/ability/inclination to really fall in love with it like some of us have. You went from a bootcamp or a degree where you might have only learned a slice of this field to a job where you still only working at the surface level of it.

The result of this can be boredom and apathy and you catch yourself wondering Wasn’t this supposed to be exciting? and Wasn’t the world full of interesting problems waiting to be solved?, well… it is! the world is full of interesting problems to be solved. This field was exciting back then, and it’s only gotten more exciting since then.

TOC

1. History of information recording: We will talk about why binary is such an incredible system and why we now use it for everything.
2. Representation: How we represent numbers using binary & how we can use numbers to represent binary in various systems (hex, decimal, octal and of-course binary)
3. Small Project: Very simple C program to take a string and output using various forms.

History of information recording

Knowing the history helps us appreciate whatever was built and gives us essential context to understand the thing at a deeper level, it helps us understand why things are the way they are today.

We go back 2000 years to the Rosetta Stone This stone was made by ancient Egyptians.
It has 3 distinct sections of inscriptions, and they all say the same thing, but in different ways.

1. Hieroglyphs: More like pictorial representations carved out in stones
2. Demotic: More like written text
3. Ancient greek

The interesting thing is, Hieroglyphs & Demotic are the exact same language, both of them are read the same. Then why bother having 2 scripts for the same language?
Hieroglyphs were originally supposed to be carved into stones. Hieroglyphs quite literally means holy carving.
Demotic was developed later in the context where more people had learned to use written language and they use it for everyday things like documents, commerce etc. Hieroglyphs wasn’t feasible for everyday use obviously. So they developed a new script particularly well suited for brushstrokes on papyrus (old paper thingi).

So at this point of history, they had 2 different ways of encoding the same language into a set of written symbols into the physical world. And we can trace the human history of encoding information all the way through from that point to where we are now.

Roughly 500 years later someone in China developed block printing, where you would carve messages into a physical piece and you would dip it in *ink and would print it, kind of like a seal.

Then over the next 100 years we would find people trying to make individual block for each character that you could combine in different combinations for printing possibly anything. Then we have typewriters and all which also affected the script that was used as well. In the past cursive handwriting used to be the most effective way to write in contrast to now where we are mostly dealing with individual printed characters.

The reason for all this yapping is to highlight the fact that encoding and representation of information evolves around the technology around us. We always strive for convenience and efficiency.
It is kind of impressive that now over the past 100 years we have been moving all of human knowledge into this one coding system BINARY.

Now in many ways this is not a very good encoding system, it has just 2 symbols, 0 & 1, it will take a long time to say anything but it has 2 major advantages, that makes it very convenient given the technology around us.

1. Having only 2 symbols makes it very easy to encode in a variety of different forms very reliably. Eg: Light pulses, charge, magnetic tape, punch cards etc.
2. Flexible: We can use binary to store many different kinds of things, it can re presented in many different ways and it has many different representations. We can use these two symbols to encode any information, text, video, photo anything!
3. Computers can be very fast with binary.

Who knows after a 100 years we might no longer be using binary as often and use some completely different form of encoding. I couldn’t guess what.

About the 2nd point, it is very important to note that we can represent(encode) and interpret(decode) different things using same set of binary symbols. This image will help you understand what I mean better.

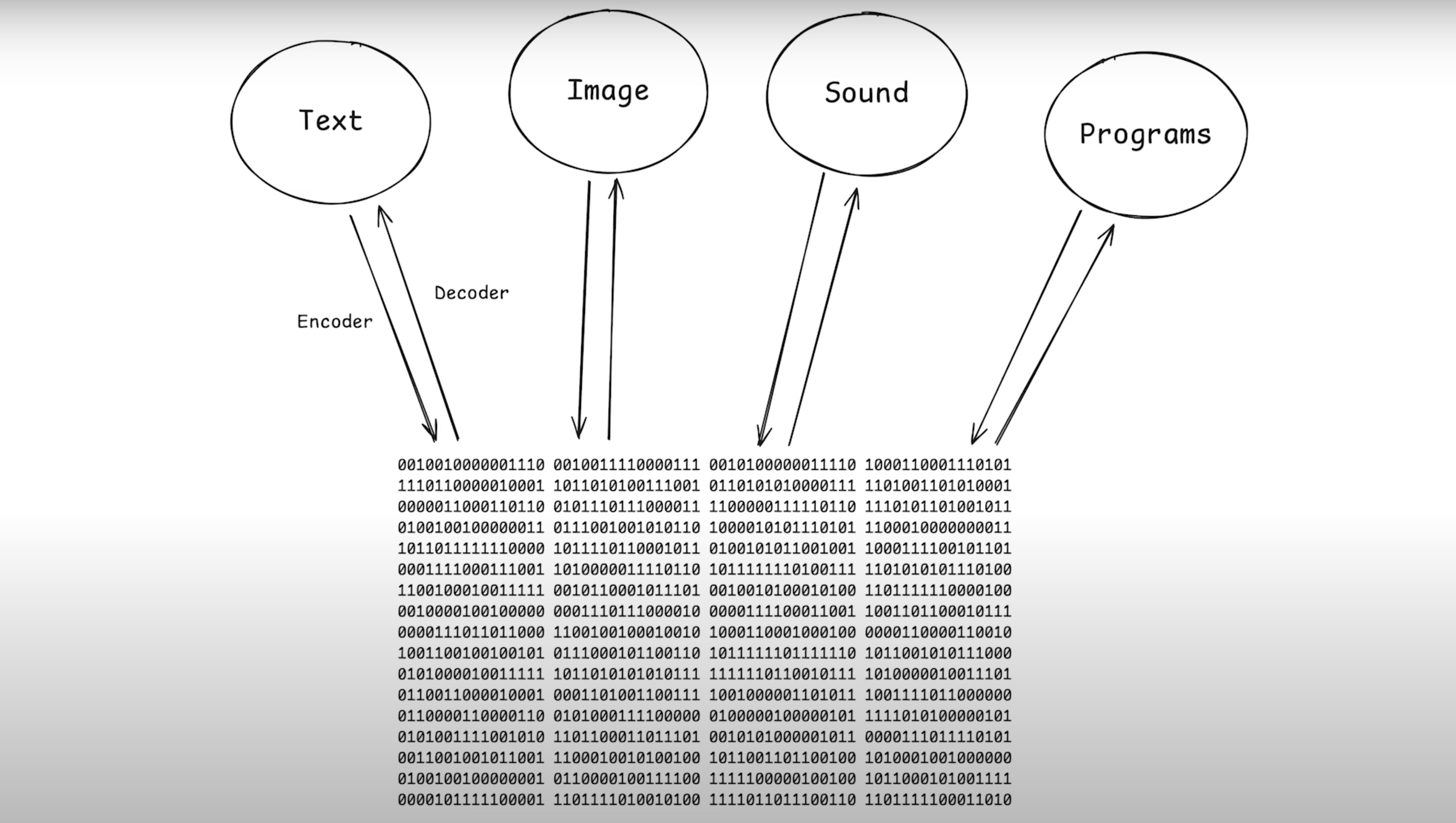
So binary can be simultaneously extremely simple and through the power of computers, extremely expressive.

Binary Numbers

Counting

Here is a nice analogy to how we count in binary.
Let’s say we count starting from 0, in our normal counting (decimal), where we have 10 counts (0-9), we can represent each number with 1 finger, since you have 10 fingers, you can count from 0 to 9.
What happens when you want to count more than 9?
Currently I am sitting at count 09, I would increment 1 to the tens place, and reset the count in our ones place. This way, I get 10, 1 incremented in the left digit, and we start counting again from 0 in the right digit. 10, 11, 12 …

In decimal, we had 10 fingers, similarly, in binary we have 2 fingers, and thus we can only have 2 counts, 0 & 1.
What if I want to count higher than one?
I add one to the higher significant digit and reset the digit where I cannot count any longer. I go from 01 to 10. Thus the counting looks like 00, 01, 10, 11, 100…

Math

In our lower classes, we all must have done expansion of numbers.
When we write 13 in decimal, we can break it down into powers of 10

The binary number 1101 (which equals 13 in decimal) can be broken down into powers of 2:

Let’s break this down step by step:

• 1 in the 2³ place: 1 × 8 = 8
• 1 in the 2² place: 1 × 4 = 4
• 0 in the 2¹ place: 0 × 2 = 0
• 1 in the 2⁰ place: 1 × 1 = 1
• Total: 8 + 4 + 0 + 1 = 13

Some interesting things

At this point I got pretty bored writing more about this because all of this seemed very easy and basic to me, the main idea of the analogy of counting with fingers and the history has been conveyed, if you wanna know more please google I’m sorry :)

Google about various other forms of encoding of binary like hexadecimal, you have 16 fingers, about ASCII etc.